Single Electron Molecule in the Variational Approach

4.5.17. Single Electron Molecule in the Variational Approach#

4.5.17.1. Motivation#

We will investigate a variational solution to possibly the simplest molecule: the H\(_2^+\) ion. This molecule only has one electron and is thus a relatively easy to solve problem. The variational solution presented is also an example of the linear combination of atomic orbitals (LCAO) to describe a molecule.

4.5.17.2. Learning Goals#

After working through these notes, you will be able to:

Write out the Hamiltonian for the H\(_2^+\) molecule (in the Born-Oppenheimer approximation)
Identify reasonable, atomic oriented, basis functions to solve for the variational solution of the H\(_2^+\) molecule
Populate the \(H\) and \(S\) matrices in a 1s basis for the H\(_2^+\) molecule
Identify the Coulomb (\(J\)) and exhange (\(K\)) integrals for the LCAO method
Describe the nature of the minimal LCAO description of bonding in the H\(_2^+\) molecule

4.5.17.3. Coding Concepts#

The following coding concepts are used in this notebook:

4.5.17.4. Background#

We would like to understand the nature of a covalent, chemical bond. This means we want to understand the energetics and spatial distributions of electrons that contribute to a covalent bond. We will use the tools of quantum mechanics in the Schrodinger picture to achieve this.

If we consider the simplest neutral molecule, H\(_2\), we have a Hamiltonian (in atomic units) that looks like

(4.908)#\[\begin{equation} \hat{H}_{H_2} = -\frac{1}{2}\nabla_1^2 - \frac{1}{r_{1A}} -\frac{1}{2}\nabla_2^2 - \frac{1}{r_{2B}} - \frac{1}{r_{1B}} - \frac{1}{r_{2A}} + \frac{1}{r_{12}} + \frac{1}{R} \end{equation}\]

where we label the two nuclei as \(A\) and \(B\) and the two electrons as \(1\) and \(2\) such that \(r_{1A}\) is the distance between nucleus \(A\) and electron 1.

The term \(\frac{1}{R}\) in the Hamiltonian above represents the Coulombic repulsion between the two positively charged nuclei. In our picture, the nuclei are fixed in space (they have no kinetic energy) and thus the distance separating them, \(R\), is also fixed.

We see that even in the Born-Oppenheimer picture of the hydrogen molecule, there are many terms we have to deal with. We will start our discussion of molecules using a simpler model molecule: H\(_2^+\). This system has two nuclei but only one electron yielding the following Hamiltonian

(4.909)#\[\begin{equation} \hat{H}_{H_2^+} = -\frac{1}{2}\nabla_1^2 - \frac{1}{r_{1A}} - \frac{1}{r_{1B}} + \frac{1}{R} \end{equation}\]

We will use the Variational Method to determine approximate ground state energies and wave functions for this system.

4.5.17.5. Trial Wave Function for H\(_2^+\)#

To start our variational approach we must propose a trial wave function. We will use linear variational parameters and propose that the electron is sitting in a combination of 1s orbitals centered on each nucleus. Namely we propose the trial wave function

(4.910)#\[\begin{equation} \phi_t(\vec{r}_1;R) = c_1 \psi_{1s_A}(\vec{r}_1) + c_2 \psi_{1s_B}(\vec{r}_1) \end{equation}\]

where \(\psi_{1s_A}\) is the 1s hydrogen atom wave function centered at the \(A\) nucleus and \(\psi_{1s_B}\) is the 1s hydrogen atom wave function centered at the \(B\) nucleus.

We will use the following shorthand in the remainder of these notes:

(4.911)#\[\begin{align} \psi_{1s_A} &\rightarrow 1s_A \\ \psi_{1s_B} &\rightarrow 1s_B \end{align}\]

The hydrogen atom wave functions are normalized

(4.912)#\[\begin{align} \left\langle 1s_A | 1s_A \right\rangle &= 1 \\ \left\langle 1s_B | 1s_B \right\rangle &= 1 \end{align}\]

but note that there is no orthogonality relationship between 1s orbitals on two different nuclei

(4.913)#\[\begin{align} \left\langle 1s_A | 1s_B \right\rangle \neq 0 \end{align}\]

Indeed it is the overlap of these two functions that will lead to any bonding behavior. We will need to determine this (and other) integrals.

4.5.17.6. Populating the \(H\) and \(S\) Matrices#

To determine the variationally optimal energy and wave function, we need to determine the variationally optimal linear coefficients \(c_1\) and \(c_2\) of the trial wave function. The procedure for this is to:

Posit the trial wave function (done)
Populate the \(H\) and \(S\) matrices
Diagonalize \(S^{-1}H\).

Here will will populate the \(2\times 2\) matrices.

4.5.17.6.1. The Overlap Matrix \(S\)#

We start with \(S\):

(4.914)#\[\begin{align} S = \begin{bmatrix} S_{11} & S_{12} \\ S_{12} & S_22 \end{bmatrix} \end{align}\]

where

(4.915)#\[\begin{align} S_{11} &= \left\langle 1s_A | 1s_A \right\rangle \\ S_{12} &= \left\langle 1s_A | 1s_B \right\rangle \\ S_{22} &= \left\langle 1s_B | 1s_B \right\rangle \end{align}\]

From normalization conditions, we know that

(4.916)#\[\begin{align} S_{11} &= 1 \\ S_{22} &= 1 \end{align}\]

We now set about determining \(S_{12}\):

(4.917)#\[\begin{align} S_{12} &= \left\langle 1s_A | 1s_B \right\rangle \\ &= \int 1s_A(\vec{r})1s_B(\vec{r})d\vec{r} \end{align}\]

This integral is somewhat involved but can be solved. Rather than doing so here I just provide the solution

(4.918)#\[\begin{equation} S_{12} = e^{-R}\left(1+R+\frac{R^2}{3}\right) \end{equation}\]

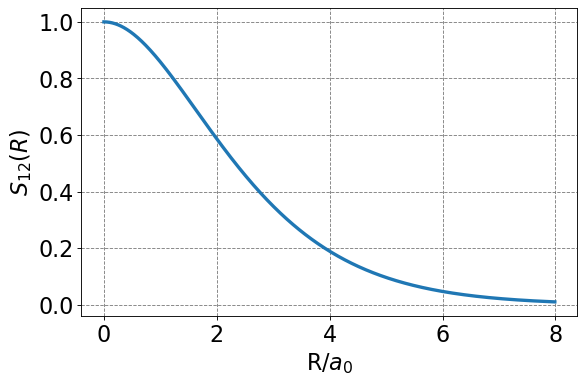
We note the \(S_{12}\) is a function of nuclear separation \(R\). This makes sense as the degree of overlap between the two 1s function will depend on then separation distance between the nuclei. We should expect no overlap when the nuclei are infinitely separated and maximal overlap when the nuclei are sitting on top of each other. Below is a plot of \(S_{12}(R)\).

../../_images/90fd76aabdd87c5efc439503d36515a39c975df57b2ebb84268e798a4ef3c61e.png

From this information we can populate the \(S\) matrix as a function of \(R\). For example, if we choose \(R=2.5\) \(a_0\) we get and \(S\) matrix of

(4.919)#\[\begin{equation} S(2.5) = \begin{bmatrix} 1 & 0.458 \\0.458 & 1 \end{bmatrix} \end{equation}\]

Below is a code snippet to populate this matrix.

S_12(2.5) =  0.45830790898343504
S(2.5) = 
[[1.         0.45830791]
 [0.45830791 1.        ]]

4.5.17.6.2. The Hamiltonian Matrix \(H\):#

The Hamiltonia matrix \(H\) is more challenging. We start with the definition

(4.920)#\[\begin{align} H = \begin{bmatrix} H_{11} & H_{12} \\ H_{12} & H_{22} \end{bmatrix} \end{align}\]

where

(4.921)#\[\begin{align} H_{11} &= \left\langle 1s_A | \hat{H} | 1s_A \right\rangle \\ H_{12} &= \left\langle 1s_A | \hat{H} | 1s_B \right\rangle \\ H_{22} &= \left\langle 1s_B | \hat{H} | 1s_B \right\rangle \end{align}\]

Each of these will need to be determined but we will be able to determine \(H_{22}\) by analogy to \(H_{11}\) since all we are doing in swapping the identity of the electron.

(4.922)#\[\begin{align} H_{11} &= \left\langle 1s_A | \hat{H} | 1s_A \right\rangle \\ &= \int 1s_A(\vec{r}) \left(-\frac{1}{2}\nabla_1^2 - \frac{1}{r_{1A}} - \frac{1}{r_{1B}} + \frac{1}{R} \right) 1s_A(\vec{r})d\vec{r} \\ &= \int 1s_A(\vec{r}) \left(-\frac{1}{2}\nabla_1^2 - \frac{1}{r_{1A}} \right) 1s_A(\vec{r})d\vec{r} + \int 1s_A(\vec{r}) \left(- \frac{1}{r_{1B}} + \frac{1}{R} \right) 1s_A(\vec{r})d\vec{r} \\ &= \int 1s_A(\vec{r}) \left(-\frac{1}{2}\nabla_1^2 - \frac{1}{r_{1A}} \right) 1s_A(\vec{r})d\vec{r} + \int 1s_A(\vec{r}) \left(- \frac{1}{r_{1B}} \right) 1s_A(\vec{r})d\vec{r} + \frac{1}{R}\int 1s_A(\vec{r})1s_A(\vec{r})d\vec{r}\\ &= E_{1s} + J + \frac{1}{R} \end{align}\]

where we recognize that the first integral is simply the 1s energy of a hydrogen atom and we define the second integral as \(J\), what is also called the Coulomb integral. That is

(4.923)#\[\begin{align} J &= \int 1s_A(\vec{r}) \left(- \frac{1}{r_{1B}} \right) 1s_A(\vec{r})d\vec{r} \\ &= -\int 1s_A(\vec{r})\frac{1}{r_{1B}}1s_A(\vec{r})d\vec{r} \end{align}\]

where that last integral becomes \(\frac{1}{R}\) because \(R\), the nuclear separation, is constant w.r.t \(\vec{r}\) and the \(1s_A\) function is normalized.

For the \(H_2^+\) case the remaining integral in \(J\) can be solved analytically. Doing so yields

(4.924)#\[\begin{align} J = e^{-2R}\left(1+\frac{1}{R}\right) - \frac{1}{R} \end{align}\]

Thus, we get that

(4.925)#\[\begin{align} H_{11} & = E_{1s} + J + \frac{1}{R}= -\frac{1}{2} + e^{-2R}\left(1+\frac{1}{R}\right) \\ H_{22} & = E_{1s} + J + \frac{1}{R}= -\frac{1}{2} + e^{-2R}\left(1+\frac{1}{R}\right) \end{align}\]

For \(H_{12}\):

(4.926)#\[\begin{align} H_{12} &= \left\langle 1s_A | \hat{H} | 1s_B \right\rangle \\ &= \int 1s_A(\vec{r}) \left(-\frac{1}{2}\nabla_1^2 - \frac{1}{r_{1A}} - \frac{1}{r_{1B}} + \frac{1}{R} \right) 1s_B(\vec{r})d\vec{r} \\ &= \int 1s_A(\vec{r}) \left(-\frac{1}{2}\nabla_1^2 - \frac{1}{r_{1A}} \right) 1s_B(\vec{r})d\vec{r} + \int 1s_A(\vec{r}) \left(- \frac{1}{r_{1B}} + \frac{1}{R} \right) 1s_B(\vec{r})d\vec{r} \\ &= \int 1s_A(\vec{r}) \left(-\frac{1}{2}\nabla_1^2 - \frac{1}{r_{1A}} \right) 1s_B(\vec{r})d\vec{r} + \int 1s_A(\vec{r}) \left(- \frac{1}{r_{1B}}\right)1s_B(\vec{r})d\vec{r} + \frac{1}{R}\int 1s_A(\vec{r}) 1s_B(\vec{r})d\vec{r} \\ &= E_{1s}S_{12} + K + \frac{S_{12}}{R} \end{align}\]

where we recognize that \(\left(-\frac{1}{2}\nabla_1^2 - \frac{1}{r_{1A}} \right) 1s_B = E_{1s}1s_B\), \(S_{12} = \langle 1s_A | 1s_B\rangle\), and have defined the exhange integral, \(K\), to be

(4.927)#\[\begin{align} K &= \int 1s_A(\vec{r}) \left(- \frac{1}{r_{1B}} \right) 1s_B(\vec{r})d\vec{r} \\ &= -\int 1s_A(\vec{r})\frac{1}{r_{1B}}1s_B(\vec{r})d\vec{r} \\ &= -e^{-R}\left(1+R\right) \end{align}\]

where the last step I have used the solution for the simple case of H\(_2^+\) but have not shown it to be true.

We can now populate the \(H\) matrix as

(4.928)#\[\begin{align} H &= \begin{bmatrix} E_{1s} + J + \frac{1}{R} & E_{1s}S_{12} + K + \frac{S_{12}}{R} \\ E_{1s}S_{12} + K + \frac{S_{12}}{R} & E_{1s} + J + \frac{1}{R}\end{bmatrix} \\ &= \left(E_{1s} + \frac{1}{R}\right)\begin{bmatrix} 1 & S_{12} \\ S_{12} & 1\end{bmatrix} + \begin{bmatrix} J & K \\ K & J \end{bmatrix} \end{align}\]

For a nuclear separation value of 2.5 Bohr, for example, this yields

(4.929)#\[\begin{equation} H(R=2.5) = \begin{bmatrix} -0.491 & -0.333 \\ -0.333 & -0.491\end{bmatrix} \end{equation}\]

Below is the code to compute this.

H(1.5) = 
[[-0.49056687 -0.33312829]
 [-0.33312829 -0.49056687]]

4.5.17.6.3. Combined Solution#

Now that we have equations for \(H\) and \(S\) in terms of \(R\) (the nuclear separation; \(S_{12}\), \(J\), and \(K\) are all functions of \(R\)), we can compute the eigenvalues and eigenvectors of \(S^{-1}H\) for a given nuclear separation distance.

Let’s choose 2.5 Bohr, for example, in which case we have

(4.930)#\[\begin{align} S(2.5) &= \begin{bmatrix} 1 & 0.458 \\0.458 & 1 \end{bmatrix} \\ H(2.5) &= \begin{bmatrix} -0.491 & -0.333 \\ -0.333 & -0.491\end{bmatrix} \\ S(2.5)^{-1}H(2.5) &= \begin{bmatrix} -0.428 & -0.138 \\ -0.138 & -0.428\end{bmatrix} \end{align}\]

Computing the eigenvalues of \(S(2.5)^{-1}H(2.5)\) yields:

(4.931)#\[\begin{equation} E(2.5) = -0.565\text{ and } -0.291 \end{equation}\]

The ground state energy is the first (minimum) of these. The corresponding eigenvectors (or vectors of variational coefficients) are

(4.932)#\[\begin{equation} v = \begin{bmatrix} -0.707 & 0.707 \\ -0.707 & -0.707\end{bmatrix} \end{equation}\]

where these are listed as column vectors meaning the that coefficients for the ground state energy are

(4.933)#\[\begin{align} c_1 &= -0.707 \\ c_2 &= -0.707 \end{align}\]

S^{-1}H(2.5) =  [[-0.4277358  -0.13709359]
 [-0.13709359 -0.4277358 ]]
Eigenvalues: [-0.56482939 -0.29064221]
Eigenvectors: [[-0.70710678  0.70710678]
 [-0.70710678 -0.70710678]]

Due to the symmetry of this problem and normalization requirements, it turns out that the coefficients must always be

(4.934)#\[\begin{align} c_1 &= \pm \frac{1}{\sqrt{2(1-S_{12})}} \\ c_2 &= \pm \frac{1}{\sqrt{2(1-S_{12})}} \end{align}\]

That is the must always be the same magnitude (symmetry) and their values are dictated by normalization (which depends on the overlap of the two basis functions).

The minimum energy state is the linear combination in which the coefficients both have the same sign. The higher energy (antibonding orbital) has the coefficients with opposing sign. These can be described as

(4.935)#\[\begin{align} \phi_+ = \frac{1}{\sqrt{2(1-S_{12})}}\left(1s_A + 1s_B\right) \\ \phi_- = \frac{1}{\sqrt{2(1-S_{12})}}\left(1s_A - 1s_B\right) \end{align}\]

4.5.17.7. Solution as a Function of \(R\)#

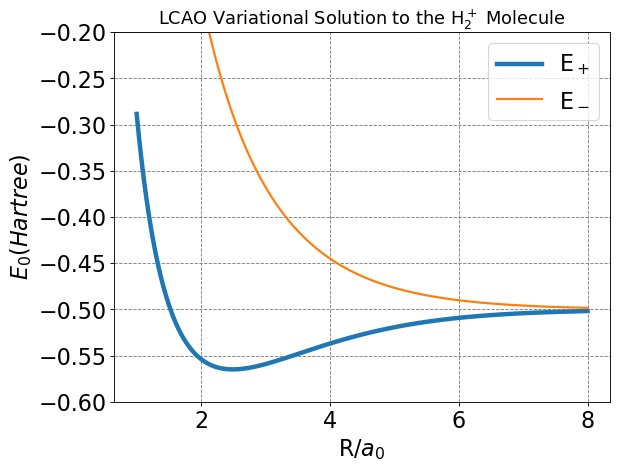
In order to investigate things such as the predicted bond length and bonding energy of this model of the H\(_2^+\) molecule, we must perform the above calculation (population of the \(H\) and \(S\) matrices and diagonalization of the \(S^{-1}H\) matrix) for various \(R\) values. The bond distance will be the value of \(R\) at the minimum energy and the bonding energy will be the difference between the energy at that position and the energy at infinite separation of the nuclei (\(-0.5\) Hartree in this case).

Below I make a plot of energies as a function of \(R\) for this model of the H\(_2^+\) molecule.

../../_images/9e3bf76f29b9fd0142d50c3e4d0d5f4227dfcba17ea9853abea493dc52eeef8c.png

Bonding energy: -0.06483 Hartree or  -40.68725 kcal/mol
Bonding distance: 2.493 Bohr

We see from the plot and code output above that the predicted bond distance for this model of H\(_2^+\) is 2.493 Bohr with a bond energy of -0.06483 Hartree (-40.7 kcal/mol).

These are not actually in great agreement with the “exact” values of 1.999 Bohr and -0.1 Hartree. But the simple approach outline here does give qualitative agreement and is a useful model for generalizing to other molecules.

We could get better agreement in a number of ways. These include:

Increasing the number of basis functions
Improving the basis functions (either by modifying them or including additional variational parameters)

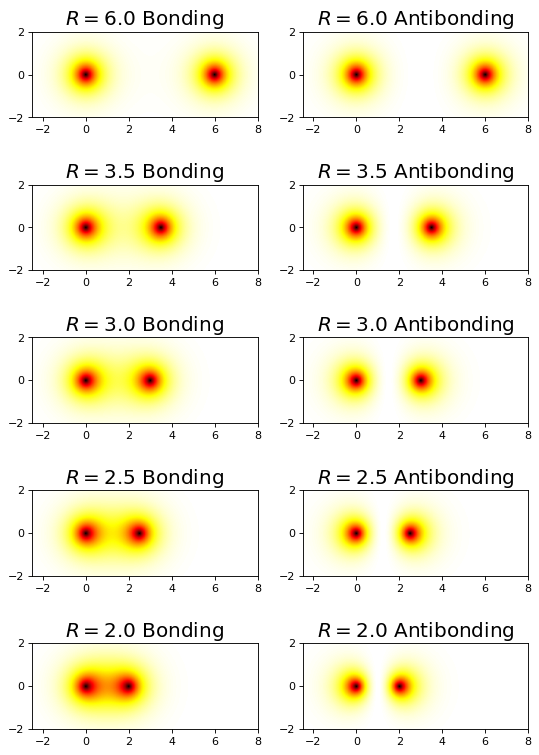
4.5.17.8. Orbital/Electron Densities#

Show code cell source Hide code cell source

# make two plots of the same spherical harmonic
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm, colors
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import sph_harm
from scipy.special import eval_genlaguerre
from scipy.special import lpmv
from scipy.special import factorial
%matplotlib inline
from scipy.optimize import root

a0 = 1.0 # radial unit of Bohr!   

def hydrogen_atom_wf(r,theta,phi,n,l,m):
    Y_norm = np.sqrt((2*l+1)*factorial(l-np.abs(m))/(4*np.pi*factorial(l+np.abs(m))))
    R_prefactor = -np.sqrt(factorial(n-l-1)/(2*n*factorial(n+l)))*(2.0/(n*a0))**(l+1.5)*np.power(r,l)*np.exp(-r/(n*a0))
    R = R_prefactor*eval_genlaguerre(n-l-1,2*l+1,2*r/(n*a0))
    return Y_norm*sph_harm(m, l, phi, theta).real*R

def h2plus_prob(r_nuc,x,y,z):
    r1 = np.sqrt(x*x + y*y + z*z)
    phi1 = np.arctan2(y,x)
    theta1 = np.arccos(z/r1)
    r2 = np.sqrt((x-r_nuc)**2 + y*y + z*z)
    phi2 = np.arctan2(y,x-r_nuc)
    theta2 = np.arccos(z/r2)
    #
    s12 = np.exp(-r_nuc)*(1+r_nuc+r_nuc**2/3)
    # 
    h2plus_wf = np.sqrt(1/(2*(1-s12)))*(hydrogen_atom_wf(r1,theta1,phi1,1,0,0) + hydrogen_atom_wf(r2,theta2,phi2,1,0,0))
    return h2plus_wf**2

def h2plus_anti_prob(r_nuc,x,y,z):
    r1 = np.sqrt(x*x + y*y + z*z)
    phi1 = np.arctan2(y,x)
    theta1 = np.arccos(z/r1)
    r2 = np.sqrt((x-r_nuc)**2 + y*y + z*z)
    phi2 = np.arctan2(y,x-r_nuc)
    theta2 = np.arccos(z/r2)
    #
    s12 = np.exp(-r_nuc)*(1+r_nuc+r_nuc**2/3)
    # 
    h2plus_wf = np.sqrt(1/(2*(1-s12)))*(hydrogen_atom_wf(r1,theta1,phi1,1,0,0) - hydrogen_atom_wf(r2,theta2,phi2,1,0,0))
    return h2plus_wf**2

def plot_h2plus_prob(r_nuc, ax_obj, r=np.linspace(0,2,20), theta=np.linspace(0,np.pi,20), phi=np.linspace(0,2*np.pi,25)):
    R, THETA, PHI = np.meshgrid(r, theta, phi)
    R = R.flatten()
    THETA = THETA.flatten()
    PHI = PHI.flatten()
    x = R*np.sin(THETA)*np.cos(PHI) 
    y = R*np.sin(THETA)*np.sin(PHI)
    z = R*np.cos(THETA)
    x = np.concatenate((x,x+r_nuc))
    y = np.concatenate((y,y))
    z = np.concatenate((z,z))
    wf = h2plus_prob(r_nuc,x,y,z)
    vmax = max(np.abs(np.amin(wf)),np.abs(np.amax(wf)))
    vmin = -vmax
    # plot
    ax_obj.set_title(rf'$R={r_nuc}$', fontsize=18)
    ax_obj.scatter3D(x,y,z,c=wf, cmap='RdBu', vmin=vmin, vmax=vmax,alpha=0.25)
    #ax_obj.set_box_aspect((100,100,100))
    ax_obj.set_axis_off()
    ax_obj.axes.xaxis.set_ticklabels([])
    ax_obj.axes.yaxis.set_ticklabels([])
    ax_obj.axes.zaxis.set_ticklabels([])
    
def plot_h2plus_prob_xz_projection(r_nuc, ax_obj):
    x = np.linspace(-2.5,8,1200)
    z = np.linspace(-2,2,600)
    X, Z= np.meshgrid(x, z)
    Y = np.zeros(X.shape)
    x = X.flatten()
    y = Y.flatten()
    z = Z.flatten()
    wf = h2plus_prob(r_nuc,x,y,z)
    wf = wf.reshape(X.shape)
    vmax = max(np.abs(np.amin(wf)),np.abs(np.amax(wf)))
    vmin = -vmax
    # plot
    ax_obj.set_title(rf'$R={r_nuc}$ Bonding', fontsize=18)
    #c = ax_obj.pcolormesh(X, Z, wf, cmap='RdBu', vmin=vmin, vmax=vmax)
    c = ax_obj.pcolormesh(X, Z, wf, cmap='hot_r',vmin=0,vmax=vmax)
    # set the limits of the plot to the limits of the data
    ax_obj.axis([-2.5, 8, -2, 2])
    ax_obj.set_aspect('equal')
    #ax_obj.set_axis_off()
    return c
def plot_h2plus_anti_prob_xz_projection(r_nuc, ax_obj):
    x = np.linspace(-2.5,8,1200)
    z = np.linspace(-2,2,600)
    X, Z= np.meshgrid(x, z)
    Y = np.zeros(X.shape)
    x = X.flatten()
    y = Y.flatten()
    z = Z.flatten()
    wf = h2plus_anti_prob(r_nuc,x,y,z)
    wf = wf.reshape(X.shape)
    vmax = max(np.abs(np.amin(wf)),np.abs(np.amax(wf)))
    vmin = -vmax
    # plot
    ax_obj.set_title(rf'$R={r_nuc}$ Antibonding', fontsize=18)
    #c = ax_obj.pcolormesh(X, Z, wf, cmap='RdBu', vmin=vmin, vmax=vmax)
    c = ax_obj.pcolormesh(X, Z, wf, cmap='hot_r',vmin=0,vmax=vmax)
    # set the limits of the plot to the limits of the data
    ax_obj.axis([-2.5, 8, -2, 2])
    ax_obj.set_aspect('equal')
    #ax_obj.set_axis_off()
    return c

../../_images/ca505d77ffe3651209053fa9dcb1958d6ccc2ce14187416b2908bb938312ec8a.png